Parabola
| Parabola, onun fokus məsafəsi və direktrisası | |

| |
| Kəsik konus: | 
|
| Eksentrisitet: | |
| Bərabərlik: | |
| Hiperbola Şablon:·w Parabola Şablon:·w Ellips Şablon:·w Çevrə | |
Parabola (Şablon:Lang-gr, tətbiq) — kvadratik funksiyanın (y = x²) qrafikinə verilən addır. Parabola Hiperbolanın tərsidir. Parabola dedikdə müstəvinin elə nöqtələrinin həndəsi yeri başa düşülür ki, bu nöqtələrin müstəvinin verilmiş düz xəttindən və verilmiş nöqtəsində olan məsafələri bir-birinə bərabər olsun. Müstəvinin verilmiş bu düz xəttinə parabolanın direktirisi, verilmiş nöqtəsinə isə parabolanın fokusu deyilir. Parabolanın fokusunu adətən ilə işarə edirlər.
Bərabərlik
Düzxətli koordinat sistemi üzərində Parabolanın kanonik şəkli aşağıdakı kimidir:
- (ya da , əgər uc nöqtələrinin yernini dəyişdirsək).
Kvadrat tənlik: при həmçinin, parabolanın и qrafikini əks etdirir, bu düstur kimi: , ancaq birinci bərabərlik ikinci bərabərlikdən ona görə fərqlənir ki, birinci bərabərliyin başlanğıcı koordinat başlanğıcı üzərində deyildir. -nın müxtəlif nöqtələri üçün koordinat aşağıdakı düsturla hesablanır:
- haradakı: — Diskriminant. Həmçinin: kvadratik tənliyi bu şəkildə də göstərilə bilər. Əgər nöqtəsi koordinat siteminin başlanğıcı üzərində olarsa kanonik şəkildə göstərilə bilər. Bu zaman: ifadəsi meydana çıxır.
Kvadrat tənliyinin əmsallarının hesablanması
Əgər tənliyi üçün tapılmış üç nöqtə üçün , , ifadələr alınarsa, onda kvadrat tənliyinin əmsallarını aşağıdakı kimi hesablamaq olar:
Digər bərabərliklər
Şaquli simmetriyanın ucları
haradakı:
- . Parametrik forması:
Üfüqi simmetriyanın ucları
haradakı:
- . Parametrik forması:
Baş parabola
Parabola üçün ümumi düstur aşağıdakı kimidir:
və aşağıdakı kimi ifadə üçün doğrudur,
- .
Baş parabola üçün fokus tənliyi: F(u, v), və a direktriks üçün düstur:
is
Qauss xəritəsinin forması
Qauss xəritəsinin forması aşağıdakı kimidir: tənliyin ifadəsi aşağıdakı ifadə kimi eynigüclüdür: .
Polyar koordinatda parabola
Polyar koordinatda olan parabola üçün aşağıdakı bərabərliklər vardır:
.
Fəzada Parabola
Bir sıra kosmik cisimlərin trayektoriyası (kometlər, asteroidlər və s.) böyük sürətlə parabolaya oxşayırlar. Parabola konus ailəsinin bir hissəsinə aiddir. Parabolanın formasından bir sıra arxitekturada istifadə edilir.
-
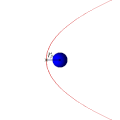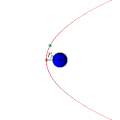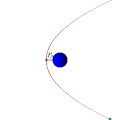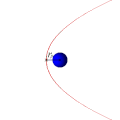
Parabolik orbit
-
Basketbol topunun düşməsi
-
-
-
-
Parabolanın konus şəkli
Həmçinin bax
Xarici keçidlər
- Animierte Parabel
- Apollonius' Derivation of the Parabola*
- Interactive parabola-drag focus, see axis of symmetry, directrix, standard and vertex forms
- Archimedes Triangle and Squaring of Parabola
- Two Tangents to Parabola
- Parabola As Envelope of Straight Lines
- Parabolic Mirror
- Three Parabola Tangents
- Module for the Tangent Parabola
- Focal Properties of Parabola
- Parabola As Envelope II
- The similarity of parabola
- Dynamic Geometry Sketches, interactive dynamic geometry sketch.
- a method of drawing a parabola with string and tacks Şablon:Vebarxiv