Loqarifm

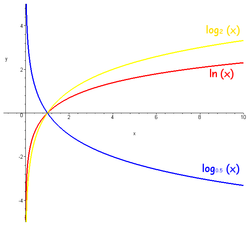
Loqarifm - b ədədini almaq üçün a əsasını yüksəltmək lazım gələn qüvvət üstünə b ədədinin a əsasına görə loqarifmi deyilir: $\log_{a} b$ . "Loqarifm" terminini elmə ilk dəfə şotlandiya alimi Con Nepyer (1550-1617) gətirmişdir.

Loqarifmik eyniliklər

Aşağıdakı cədvəlin 1-ci tərəfində düstur, 2-ci tərəfində isə bu düsturlara aid misallar verilmişdir:

	Düstur	Misal
Vurma	$\log_{b} (x y) = \log_{b} (x) + \log_{b} (y)$	$\log_{3} (243) = \log_{3} (9 \cdot 27) = \log_{3} (9) + \log_{3} (27) = 2 + 3 = 5$
Bölmə	$\log_{b} (\frac{x}{y}) = \log_{b} (x) - \log_{b} (y)$	$\log_{2} (16) = \log_{2} (\frac{64}{4}) = \log_{2} (64) - \log_{2} (4) = 6 - 2 = 4$
Yüksəltmə	$\log_{b} (x^{p}) = p \log_{b} (x)$	$\log_{2} (64) = \log_{2} (2^{6}) = 6 \log_{2} (2) = 6$
Kökaltı ifadə	$\log_{b} \sqrt[p]{x} = \frac{\log_{b} (x)}{p}$	$\log_{10} \sqrt{1000} = \frac{1}{2} \log_{10} 1000 = \frac{3}{2} = 1.5$

Xarici keçidlər

Loqarifm

Loqarifmik eyniliklər

Xarici keçidlər

Naviqasiya menyusu

Axtar